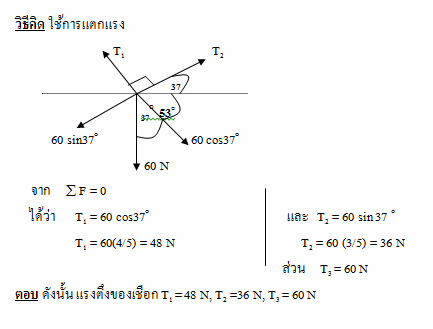
การหาแรงตึงเชือก
หลักการ
1. เชือกเส้นเดียวกันแรงตีงเชือกย่อมเท่ากัน
2. แรงตึงเชีอกมีทิศพุ่งออกจากจุดที่เราพิจารณา
3. รอกลื่นทำให้เชือกเปลี่ยนทิศทางเท่านั้นไม่มีผลต่อขนาดของแรงที่กระทำ
วันเสาร์ที่ 3 กันยายน พ.ศ. 2559
กฎของนิวตัน
กฎข้อที่ 1 กฎของความเฉื่อย (Inertia)
"วัตถุที่หยุดนิ่งจะพยายามหยุดนิ่งอยู่กับที่ตราบที่ไม่มีแรงภายนอกมากระทำ ส่วนวัตถุที่เคลื่อนที่จะเคลื่อนที่เป็นเส้นตรงด้วยความเร็วคงที่ตราบที่ไม่มีแรงภายนอกมากระทำเช่นกัน"
กฎข้อที่ 2 กฎของแรง (Force)
"ความเร่งของวัตถุแปรผันตามแรงที่กระทำต่อวัตถุ แต่แปรผกผันกับมวลของวัตถุ”
• ถ้าเราผลักวัตถุให้แรงขึ้น ความเร่งของวัตถุก็จะมากขึ้นตามไปด้วย
• ถ้าเราออกแรงเท่าๆ กัน ผลักวัตถุสองชนิดซึ่งมีมวลไม่เท่ากัน วัตถุที่มีมวลมากจะเคลื่อนที่ด้วยความเร่งน้อยกว่าวัตถุที่มีมวลน้อย
ความเร่งของวัตถุ = แรงที่กระทำต่อวัตถุ / มวลของวัตถุ (หรือ a = F/m)
กฎข้อที่ 3 กฎของแรงปฏิกิริยา
"แรงที่วัตถุที่หนึ่งกระทำต่อวัตถุที่สอง ย่อมเท่ากับ แรงที่วัตถุที่สองกระทำต่อวัตถุที่หนึ่ง แต่ทิศทางตรงข้ามกัน” หรือกล่าวอย่างสั้นๆ ว่า แรงกริยาเท่ากับแรงปฏิกิริยา (Action = Reaction) โดยที่แรงทั้งสองจะเกิดขึ้นพร้อมกัน นิวตันอธิบายว่า ขณะที่ดวงอาทิตย์มีแรงกระทำต่อดาวเคราะห์ ดาวเคราะห์ก็มีแรงกระทำต่อดวงอาทิตย์ ในปริมาณที่เท่ากันแต่มีทิศทางตรงกันข้าม และนั่นคือแรงดึงดูดร่วม
"วัตถุที่หยุดนิ่งจะพยายามหยุดนิ่งอยู่กับที่ตราบที่ไม่มีแรงภายนอกมากระทำ ส่วนวัตถุที่เคลื่อนที่จะเคลื่อนที่เป็นเส้นตรงด้วยความเร็วคงที่ตราบที่ไม่มีแรงภายนอกมากระทำเช่นกัน"
กฎข้อที่ 2 กฎของแรง (Force)
"ความเร่งของวัตถุแปรผันตามแรงที่กระทำต่อวัตถุ แต่แปรผกผันกับมวลของวัตถุ”
• ถ้าเราผลักวัตถุให้แรงขึ้น ความเร่งของวัตถุก็จะมากขึ้นตามไปด้วย
• ถ้าเราออกแรงเท่าๆ กัน ผลักวัตถุสองชนิดซึ่งมีมวลไม่เท่ากัน วัตถุที่มีมวลมากจะเคลื่อนที่ด้วยความเร่งน้อยกว่าวัตถุที่มีมวลน้อย
ความเร่งของวัตถุ = แรงที่กระทำต่อวัตถุ / มวลของวัตถุ (หรือ a = F/m)
กฎข้อที่ 3 กฎของแรงปฏิกิริยา
"แรงที่วัตถุที่หนึ่งกระทำต่อวัตถุที่สอง ย่อมเท่ากับ แรงที่วัตถุที่สองกระทำต่อวัตถุที่หนึ่ง แต่ทิศทางตรงข้ามกัน” หรือกล่าวอย่างสั้นๆ ว่า แรงกริยาเท่ากับแรงปฏิกิริยา (Action = Reaction) โดยที่แรงทั้งสองจะเกิดขึ้นพร้อมกัน นิวตันอธิบายว่า ขณะที่ดวงอาทิตย์มีแรงกระทำต่อดาวเคราะห์ ดาวเคราะห์ก็มีแรงกระทำต่อดวงอาทิตย์ ในปริมาณที่เท่ากันแต่มีทิศทางตรงกันข้าม และนั่นคือแรงดึงดูดร่วม
การเคลื่อนที่ในแนวเส้นตรง
การเคลื่อนที่ในแนวเส้นตรง แบ่งเป็น 2 แบบ คือ
1. การเคลื่อนที่ในแนวเส้นตรงที่ไปทิศทางเดียวกันตลอด เช่น โยนวัตถุขึ้นไปตรงๆ รถยนต์ กำลังเคลื่อนที่ไปข้างหน้าในแนวเส้นตรง
2. การเคลื่อนที่ในแนวเส้นเส้นตรง แต่มีการเคลื่อนที่กลับทิศด้วย เช่น รถแล่นไปข้างหน้าในแนวเส้นตรง เมื่อรถมีการเลี้ยวกลับทิศทาง ทำให้ทิศทางในการเคลื่อนที่ตรงข้ามกัน
การเคลื่อนที่ในแนวเส้นตรง แบ่งเป็น 2 แบบ คือ
1. การเคลื่อนที่ในแนวเส้นตรงที่ไปทิศทางเดียวกันตลอด เช่น โยนวัตถุขึ้นไปตรงๆ รถยนต์ กำลังเคลื่อนที่ไปข้างหน้าในแนวเส้นตรง
2. การเคลื่อนที่ในแนวเส้นเส้นตรง แต่มีการเคลื่อนที่กลับทิศด้วย เช่น รถแล่นไปข้างหน้าในแนวเส้นตรง เมื่อรถมีการเลี้ยวกลับทิศทาง ทำให้ทิศทางในการเคลื่อนที่ตรงข้ามกัน
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ แบ่งออกเป็น 2 ลักษณะ ดังนี้
-เมื่อมีเวกเตอร์ย่อย 2 เวกเตอร์
-เมื่อมีเวกเตอร์ย่อยมากกว่า 2 เวกเตอร์
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ หรอืมีเวกเตอร์ย่อย 2 เวกเตอร์
-กรณีเวกเตอร์ทั้งสองไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของเวกเตอร์ทั้งสองทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ทั้งสอง
-กรณีเวกเตอร์ทั้งสองสวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของขนาดเวกเตอร์ทั้งสองทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ แบ่งออกเป็น 2 ลักษณะ ดังนี้
-เมื่อมีเวกเตอร์ย่อย 2 เวกเตอร์
-เมื่อมีเวกเตอร์ย่อยมากกว่า 2 เวกเตอร์
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ หรอืมีเวกเตอร์ย่อย 2 เวกเตอร์
-กรณีเวกเตอร์ทั้งสองไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของเวกเตอร์ทั้งสองทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ทั้งสอง
-กรณีเวกเตอร์ทั้งสองสวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของขนาดเวกเตอร์ทั้งสองทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
การหาเวกเตอร์ลัพธ์
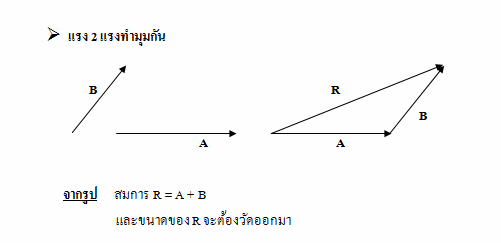
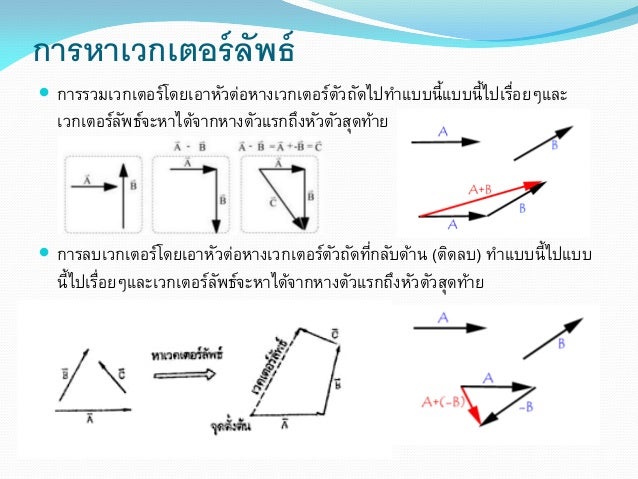
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีดังนี้
(1) เขียนลูกศรของเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
(2) นำหางลูกศรของเวกเตอร์สองต่อกับหัวลูกศรของเวกเตอร์แรก
(3) ถ้ามีเวกเตอร์ย่อยๆอีกให้ทำตามขั้นตอนที่ 2 จนครบ
(4) เวกเตอร์ลัพธ์ หาได้จากลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวลูกศรของเวกเตอร์อันสุดท้าย
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีดังนี้
(1) เขียนลูกศรของเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
(2) นำหางลูกศรของเวกเตอร์สองต่อกับหัวลูกศรของเวกเตอร์แรก
(3) ถ้ามีเวกเตอร์ย่อยๆอีกให้ทำตามขั้นตอนที่ 2 จนครบ
(4) เวกเตอร์ลัพธ์ หาได้จากลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวลูกศรของเวกเตอร์อันสุดท้าย
ปริมาณทางฟิสิกส์
ปริมาณ (Quantity)
วิทยาศาสตร์เป็นวิชาที่ศึกษาเกี่ยวกับความจริงที่สามารถพิสูจน์ได้ด้วยกระบวนการทางวิทยาศาสตร์ นำความรู้ที่ได้จากการศึกษาทดลอง จดบัทึกมารวบรวมเป็นกฎ ทฤษฎี เพื่อเป็นความรู้ในการอธิบายปรากฎการณ์ต่างๆ ที่เกิดขึ้น ซึ่งการศึกษาวิทยาศาสร์เป็นการศึกษา2 ส่วนคือ เชิงคุณภาพ เป็นการศึกษาบรรยายเชิงข้อมูลพรรณนา ตามสภาพการรับรู้ของมนุษย์ เช่น การบรรยายรูปลักษณะ สี กลิ่น รส และเชิงปริมาณ เป็นการศึกษาข้อมูลเชิงตัวเลข ซึ่งได้จากการสังเกต และเครื่องมือวัด เช่น ความยาว มวล เวลา ปริมาณต่างๆ ที่เกี่ยวข้องกับวิชาฟิสิกส์แบ่งออกได้เป็น
ปริมาณในทางฟิสิกส์ มี 2 ปริมาณ คือ
1. ปริมาณสเกลาร์ (Scalar) เป็นปริมาณที่บอกขนาดเพียงอย่างเดียว เช่น มวล , อัตราเร็ว , พลังงาน ฯลฯ
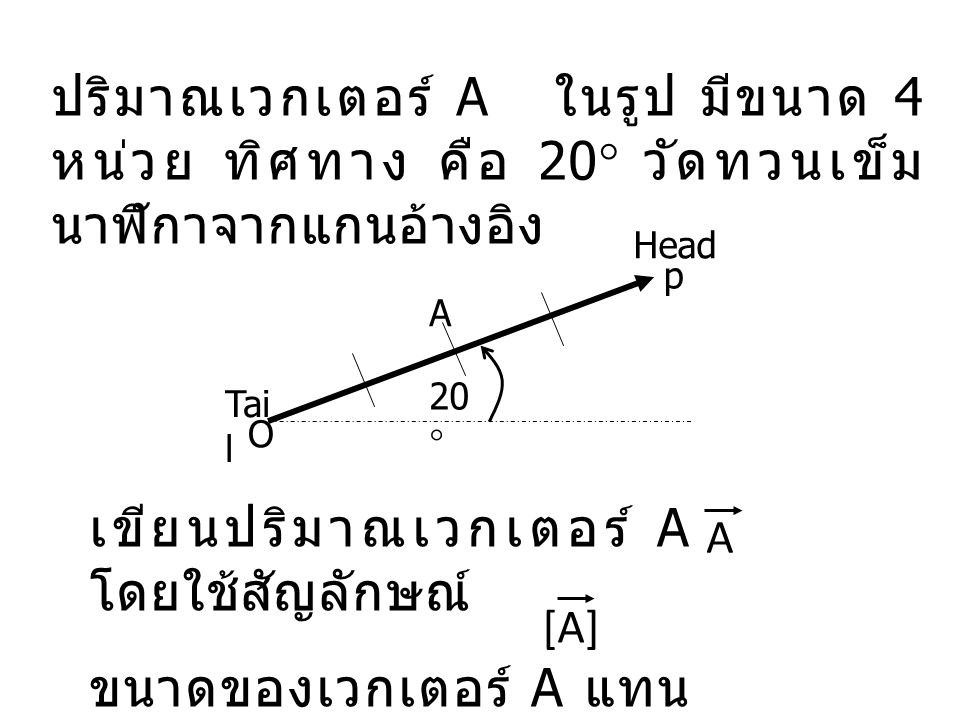
2. ปริมาณเวกเตอร์ (Vector) เป็นปริมาณที่บอกทั้งขนาดและทิศทาง เช่น ความเร็ว , ความเร่ง , การกระจัด , แรง ฯลฯ อ่านเพิ่มเติม
ปริมาณ (Quantity)
วิทยาศาสตร์เป็นวิชาที่ศึกษาเกี่ยวกับความจริงที่สามารถพิสูจน์ได้ด้วยกระบวนการทางวิทยาศาสตร์ นำความรู้ที่ได้จากการศึกษาทดลอง จดบัทึกมารวบรวมเป็นกฎ ทฤษฎี เพื่อเป็นความรู้ในการอธิบายปรากฎการณ์ต่างๆ ที่เกิดขึ้น ซึ่งการศึกษาวิทยาศาสร์เป็นการศึกษา2 ส่วนคือ เชิงคุณภาพ เป็นการศึกษาบรรยายเชิงข้อมูลพรรณนา ตามสภาพการรับรู้ของมนุษย์ เช่น การบรรยายรูปลักษณะ สี กลิ่น รส และเชิงปริมาณ เป็นการศึกษาข้อมูลเชิงตัวเลข ซึ่งได้จากการสังเกต และเครื่องมือวัด เช่น ความยาว มวล เวลา ปริมาณต่างๆ ที่เกี่ยวข้องกับวิชาฟิสิกส์แบ่งออกได้เป็น
ปริมาณในทางฟิสิกส์ มี 2 ปริมาณ คือ
1. ปริมาณสเกลาร์ (Scalar) เป็นปริมาณที่บอกขนาดเพียงอย่างเดียว เช่น มวล , อัตราเร็ว , พลังงาน ฯลฯ
2. ปริมาณเวกเตอร์ (Vector) เป็นปริมาณที่บอกทั้งขนาดและทิศทาง เช่น ความเร็ว , ความเร่ง , การกระจัด , แรง ฯลฯ อ่านเพิ่มเติม
แบบฝึกหัดเลขนัยสำคัญ
ผลลัพธ์ของ 16.74+5.1 มีจำนวนเลขนัยสำคัญเท่ากับตัวเลขในข้อใด
1. -3.14 2. 0.003 3. 99.99 4. 270.00
วิธีคิด
การบวก ลบเลขนัยสำคัญ ผลลัพธ์ที่ได้จะมีจำนวนตัวเลขหลังจุดทศนิยม เท่ากับจำนวนตัวเลขหลังจุดทศนิยมที่น้อยที่สุดของ ตัวเลขชุดนั้น ดังนั้น 16.74+5.1 = 21.84 ควรบันทึกเป็น 21.8 ซึ่งมีจำนวนเลขนัยสำคัญเท่ากับ 3 ตัว
ข้อ 1 มีจำนวนเลขนัยสำคัญเท่ากับ 3 ตัว เป็นคำตอบที่ถูกต้อง
ข้อ 2 , 3 , 4 มีจำนวนเลขนัยสำคัญเท่ากับ 1 , 4 , 5 ตัวตามลำดับ
ผลลัพธ์ของ 16.74+5.1 มีจำนวนเลขนัยสำคัญเท่ากับตัวเลขในข้อใด
1. -3.14 2. 0.003 3. 99.99 4. 270.00
วิธีคิด
การบวก ลบเลขนัยสำคัญ ผลลัพธ์ที่ได้จะมีจำนวนตัวเลขหลังจุดทศนิยม เท่ากับจำนวนตัวเลขหลังจุดทศนิยมที่น้อยที่สุดของ ตัวเลขชุดนั้น ดังนั้น 16.74+5.1 = 21.84 ควรบันทึกเป็น 21.8 ซึ่งมีจำนวนเลขนัยสำคัญเท่ากับ 3 ตัว
ข้อ 1 มีจำนวนเลขนัยสำคัญเท่ากับ 3 ตัว เป็นคำตอบที่ถูกต้อง
ข้อ 2 , 3 , 4 มีจำนวนเลขนัยสำคัญเท่ากับ 1 , 4 , 5 ตัวตามลำดับ
เลขนัยสำคัญ
หลักการนับเลขนัยสำคัญ
-ถ้าอยู่ในรูปจำนวนเลขทศนิยมให้เริ่มนับตัวเลขแรกที่เป็นเลขโดด (1 ถึง 9) ตัวเลขถัดไปนับหมดทุกตัว เช่น 0.561, 5.02, 10.00, 0.50 มีจำนวนเลขนัยสำคัญ 3, 3, 2, 4 และ 2 ตัว ตามลำดับ
-ถ้าวอยู่ในรูป เมื่อ (1 A < 10) และ n เป็นเลขจำนวนเต็ม ให้พิจารณาที่ค่า A เท่านั้นโดยใช้หลักเหมือนกับข้อ 1 โดยไม่ต้องคำนึงถึง n เช่น , (หรือ ), (หรือ ), (หรือ ) มีเลขนัยสำคัญ 2, 2, 4 และ 2 ตัว ตามลำดับ
-ถ้าอยู่ในรูปจำนวนเต็มให้นับหมดทุกตัวเช่น 16, 125, 5134, 60251 มีจำนวนเลขนัยสำคัญ 2, 3, 4, และ 5 ตามลำดับ แต่ถ้าเลขตัวท้าย ๆ เป็นเลขศูนย์ ต้องจัดให้อยู่ในรูป แล้วตอบตามรูปของการจัดเท่าที่เป็นไปได้ โดยมีความหมายเหมือนเดิม อ่านเพิ่มเติม
หลักการนับเลขนัยสำคัญ
-ถ้าอยู่ในรูปจำนวนเลขทศนิยมให้เริ่มนับตัวเลขแรกที่เป็นเลขโดด (1 ถึง 9) ตัวเลขถัดไปนับหมดทุกตัว เช่น 0.561, 5.02, 10.00, 0.50 มีจำนวนเลขนัยสำคัญ 3, 3, 2, 4 และ 2 ตัว ตามลำดับ
-ถ้าวอยู่ในรูป เมื่อ (1 A < 10) และ n เป็นเลขจำนวนเต็ม ให้พิจารณาที่ค่า A เท่านั้นโดยใช้หลักเหมือนกับข้อ 1 โดยไม่ต้องคำนึงถึง n เช่น , (หรือ ), (หรือ ), (หรือ ) มีเลขนัยสำคัญ 2, 2, 4 และ 2 ตัว ตามลำดับ
-ถ้าอยู่ในรูปจำนวนเต็มให้นับหมดทุกตัวเช่น 16, 125, 5134, 60251 มีจำนวนเลขนัยสำคัญ 2, 3, 4, และ 5 ตามลำดับ แต่ถ้าเลขตัวท้าย ๆ เป็นเลขศูนย์ ต้องจัดให้อยู่ในรูป แล้วตอบตามรูปของการจัดเท่าที่เป็นไปได้ โดยมีความหมายเหมือนเดิม อ่านเพิ่มเติม
คำอุปสรรค์ (prefixes)
คำอุปสรรค (prefixes) เมื่อค่าในหน่วยฐานหรือหน่วยอนุพัทธ์น้อยหรือมากเกินไปเราอาจเขียนค่านั้นอยู่ในรูปตัวเลขคูณ ด้วย ตัวพหุคูณ (ตัวพหุคูณ คือ เลขสิบยกกำลังบวกหรือลบ) ได้ เช่น ระยะทาง 0.002 เมตร เขียนเป็น เมตร แทนด้วยคำอุปสรรค มิลลิ(m) ดังนั้นระยะทาง 0.002 เมตร อาจเขียนได้ว่า 2 มิลลิเมตร คำอุปสรรคที่ใช้แทนตัวพหุคูณและสัญลักษณ์ อ่านเพิ่มเติม
คำอุปสรรค (prefixes) เมื่อค่าในหน่วยฐานหรือหน่วยอนุพัทธ์น้อยหรือมากเกินไปเราอาจเขียนค่านั้นอยู่ในรูปตัวเลขคูณ ด้วย ตัวพหุคูณ (ตัวพหุคูณ คือ เลขสิบยกกำลังบวกหรือลบ) ได้ เช่น ระยะทาง 0.002 เมตร เขียนเป็น เมตร แทนด้วยคำอุปสรรค มิลลิ(m) ดังนั้นระยะทาง 0.002 เมตร อาจเขียนได้ว่า 2 มิลลิเมตร คำอุปสรรคที่ใช้แทนตัวพหุคูณและสัญลักษณ์ อ่านเพิ่มเติม
สมัครสมาชิก:
ความคิดเห็น (Atom)